Share
What a Mathematician Says About “Lens Compression” in Photography
Our friends at Fstoppers recently created a video to explain “How Lens Compression and Perspective Distortion Work.” “Lens compression” has...

Our friends at Fstoppers recently created a video to explain “How Lens Compression and Perspective Distortion Work.”
“Lens compression” has been a contentious phrase in photography with photographers offering a range of explanations for the phenomenon, or lack thereof. DPReview’s DL Cade wrote:
We’ve been saying for years that the term “lens compression” is misleading…The main issue with the term “lens compression” is that the distortion the term refers to has nothing to do with the lens itself. The issue is simply perspective distortion.
Despite the compelling video, there wasn’t much of a consensus among the commenters, but a few made references to a branch of mathematics called “projective geometry,” a form of geometry that found many roots in perspective art. So rather than debate the semantics of “lens compression,” I decided to reach out to a mathematician.
Dr. Fumiko Futamura is a Professor of Mathematics at Southwestern University who specializes in projective geometry. She was the 2018 Recipient of the MAA Carl B. Allendoerfer Award for expository excellence of papers published in Mathematic Magazine in 2017, and has tried to make her branch of math more accessible to non-mathematicians. Here’s a TED-Ed video she created about mathematics of sidewalk illusions.
***
Some of the controversy seems to be semantic. The video states “lens compression” is a misleading term, and that perspective “distortion” (or perhaps just “perspective”) is more accurate. Is there a standard nomenclature in mathematics for this observed effect?
I do not know of any standard nomenclature in mathematics for this kind of phenomenon. I would agree that “lens compression” is a misleading term because it has more to do with the viewing angle and associated field of view.
The “thesis” of the video states that the camera’s distance to the subject and background is the cause of the “distortion.” In their example, they photograph a man’s head using different lenses (focal lengths) and distances to maintain his angular diameter. Why can’t we see his ears when he’s close to the camera? And why does his face seem to “flatten” as we move away?
This is true. I made an interactive GeoGebra graphic explaining this. https://ggbm.at/UJvCZjnW
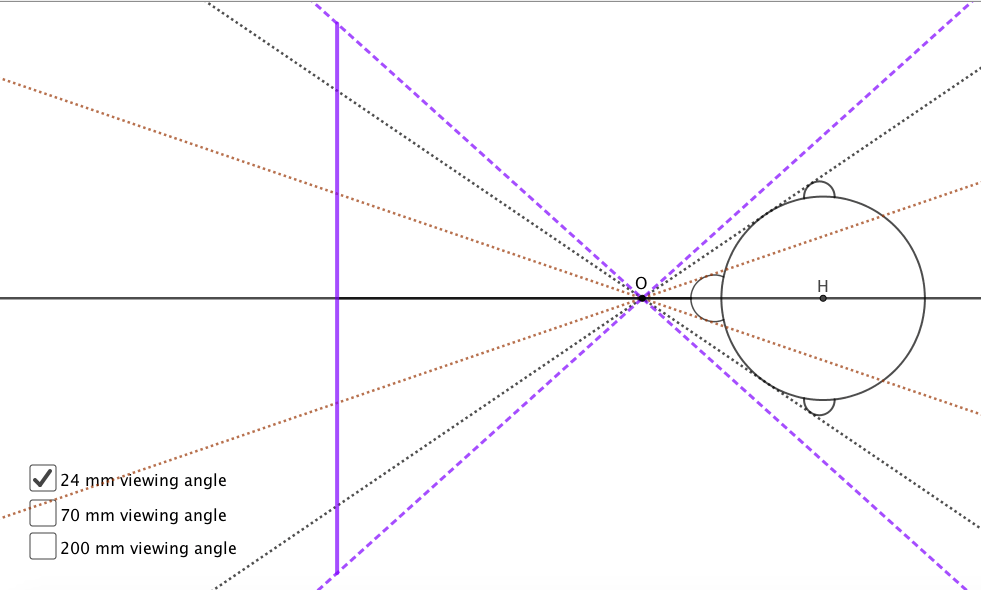
Illustration by Dr. Fumiko Futamura
When he is really close (which you can only photograph with a wide angle lens, like 24mm [to fit his entire head]), the sight line from O will be angled such that his ears are not visible, since they are behind his cheeks. The large angles also make his nose huge, taking up half his face. We are never this close to people, so it looks distorted to us.
Getting that close to the camera is not possible with a telephoto lens, like a 200mm. You have to move further back to get his head in the frame, and this decreases the angle made by the tangent lines from O to his head. Now we are able to see his ears, and his nose is now about 25% of his face, which is close to the 23% if we were to flatten his face (draw parallel lines tangent to his head and nose instead of lines through O). The further away he is, the more these tangent lines from O flatten out to be more like parallel lines, which gives that flattening effect.
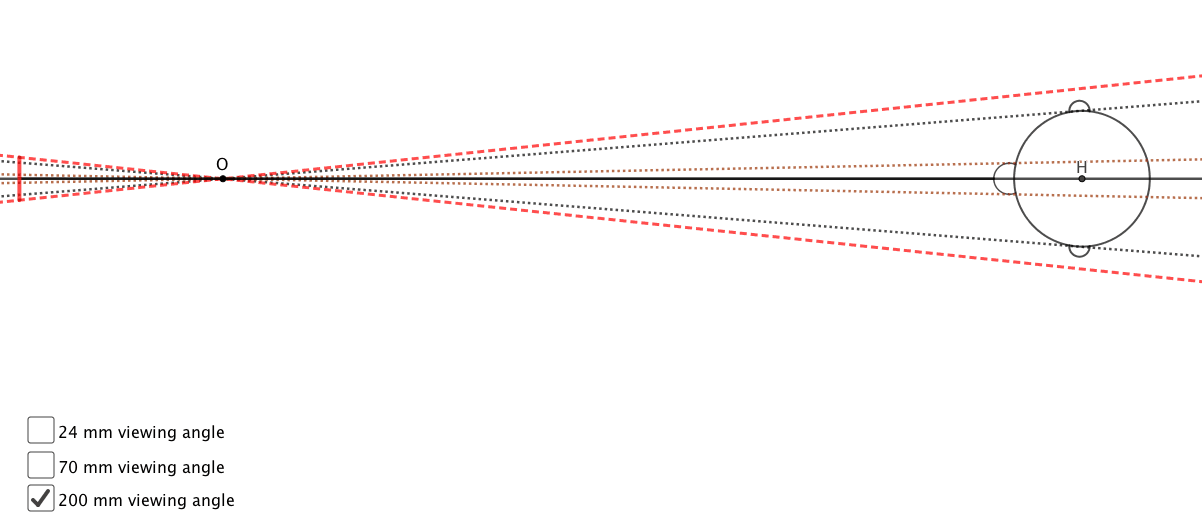
Illustration by Dr. Fumiko Futamura
One commenter wrote: “It is neither the focal length nor the camera to subject distance that causes the effect: it is actually the viewing distance to the image. There is even a subset of mathematics about this: projection [sic] geometry. The reason focal length is thought to produce the effect is that at any given print size what is known as correct viewing distance changes with focal length used. The wide-angle effect is caused by a greater viewing distance in proportion to the taking distance – if you view the same image at a closer distance in relation to the focal length/format size then the stretching that appears at the edges is not perceived. The opposite is true with the apparent compression from long focal length lenses. This is purely a perceptual problem.” How accurate is this comment?
This is not something that is studied in projective geometry. The idea of viewing distance is important, but not relevant to this particular phenomenon because for a photograph, the viewing target (the point on the photograph where your eye should be in front of to view it correctly) is in the center, and when we look at a distorted face with a large nose, the face is in the center. Viewing distance becomes important in talking about distortions on the periphery. This isn’t the best pic, but something I just had – inside the circle determined by the viewing distance, the tiles look more natural. Outside, the tiles (which are square) are greatly distorted. This is more of an anamorphic effect, but has nothing to do with lens compression.

To give you another example: in this photo taken with a wide angle lens, you can see that the columns look like they have elliptical cross sections though they actually have circular cross sections.

Photo by Ib Rasmussen (CC0 – Public Domain)
These columns are far away from the viewing target, which is the point where everything converges. Another weird thing that’s happening, the circle of lights actually looks circular, although you’re not directly under it. We just sent off a paper to a journal about this phenomenon. It’s pretty cool.
Thinking about this subject is probably not a daily topic for most people. But I came across this article about how the distortion in selfies (wide angle lens and close proximity of the camera to the face) has led to an increase in rhinoplasty. The article distills the problem into distance to subject, “When a camera lens is very close to your face, your nose is nearer to the camera relative to the rest of your face, and will therefore look larger. But when you step away from the camera, the relative distance between your nose and the rest of the face flattens — making your nose appear more proportionate.” Is this ultimately what we’re talking about? The relative size of objects in a scene compared to our expectation/memory of what they should appear like is the perspective distortion?
Oh that’s unfortunate (the part about rhinoplasty). Yes, that is what we are ultimately talking about. The phenomenon of background objects appearing larger with a telephoto lens, well, that’s just because of the smaller viewing angle. Look at how huge this block will look with a 200 mm lens on the photo (the line on the left),
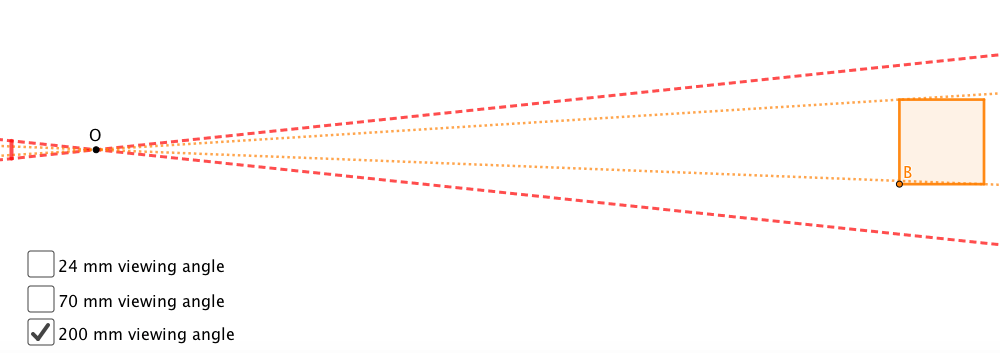
Illustration by Dr. Fumiko Futamura
vs. how small with a 70 mm lens. It will appear further away because it is smaller. And of course, if you crop the photo, it will look the same as the photo taken with a 200 mm lens (though there may be differences in things being in and out of focus).
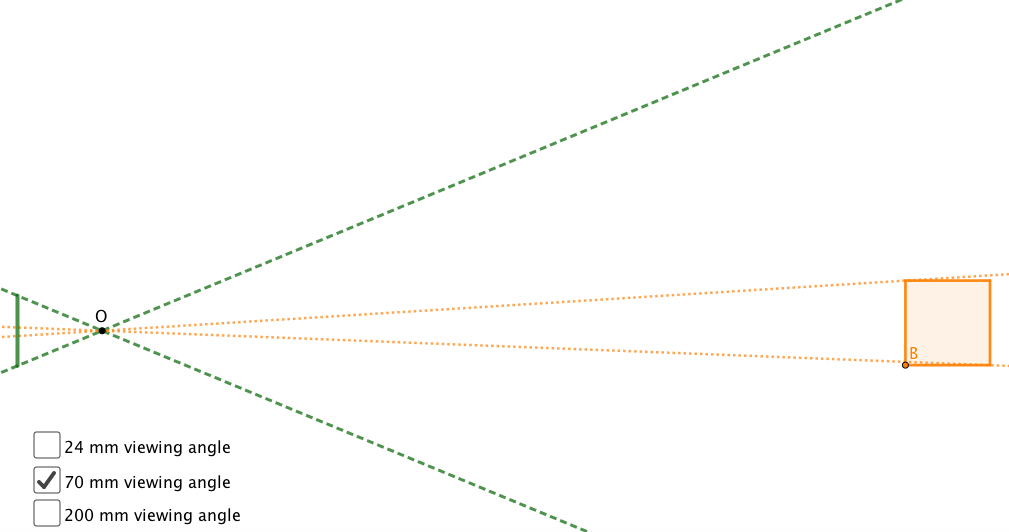
Illustration by Dr. Fumiko Futamura
These images are a simplified version of what happens with a camera – really the lens bends light rays in, so these pictures are not completely accurate. However, it still shows what’s going on. The shorter focal length allows for a wider field of view, which allows more of the scene to be pictured, and also allows for subjects to get closer to the camera.
This interview has been lightly edited for clarity.


